虚数

虚数(imaginary number)とは

理念的な数という意味でこの名が用いられている。

虚数は，2次あるいは3次の方程式を解くときに，

負数の平方根の形を導入しなければならないところから起った。

実数の範囲では負の数の平方根は求められない。

たとえば、二次方程式x²＝－1は、実数の範囲では解くことができない。

そこで、2乗すれば－1になる数を考えて、

それをiという記号で表す。


すなわち、

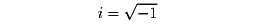
となる新しい数を導入すれば、

すべての二次方程式を解くことができる。

このiを虚数単位とよび、

a、bを任意の実数としてa＋biの形に表される数を複素数という。

ここで、b≠0である複素数を虚数（想像上の数）といい


とくにa＝0, b≠0である複素数biを純虚数という。

実数は、複素数a＋biのb＝0の場合をさしていい、

したがって、実数は複素数のなかに含まれる。





いまi という数を導入し，i ²＝－1 と定める。

この性質をもつ i を虚数単位と呼ぶ。実数 b とこの i によって，

bi という形で表現された数を虚数という。

また，a ，b を実数として，a＋bi の形の数をつくると，これは複素数であるが，これを虚数ということもある。


その場合は，bi の形の数を純虚数という。

虚数が形式的に活用されるようになったのは 18世紀だが，

19世紀の初期になって複素数を幾何学的に表現することができるようになり，

虚数の実在性，有効性が認められるようになった。