曲線

１、曲線とは

平面、あるいは空間内で、その点の座標が

一つの実変数tの連続関数となっているものを曲線、または連続曲線という。


平面内の曲線を平面曲線といい、方程式x＝f(t), y＝g(t)で表される。


空間内の曲線を空間曲線といい、x＝f(t), y＝g(t), z＝h(t)で表される。



　曲線はまた、F(x, y)＝0あるいはF(x, y, z)＝0, G(x, y, z)＝0の形で与えられることもある。


たとえば円は、





x＝r cos t , y＝r sin t  あるいは x²＋y²＝r² の形で与えられる。


　平面曲線はまた、y＝u(x)あるいは極座標によって

r＝v(θ)で与えられることもある。以下では、おもに平面曲線を考える。


　「アステロイド」「カージオイド」「クロソイド」「コンコイド」

「サイクロイド」「疾走線(しっそうせん)」「トラクトリックス」

「螺線(らせん)」「リマソン」などの個々の曲線については、各項目を参照されたい。


［竹之内脩］

2、滑らかな曲線

平面曲線x＝f(t), y＝g(t)において、

f(t), g(t)が導関数を有し、かつそれらが連続であるとき、この曲線を滑らかな曲線という。

そして、f′(t), g′(t)を成分とするベクトル(f′(t), g′(t))を接ベクトルという。


滑らかな曲線とは接ベクトルが連続的に変わっていく曲線、という意味である。

接ベクトルは、曲線上の近い2点　P(t)＝(f(t), g(t))　P(t＋Δt)＝(f(t＋Δt), g(t＋Δt))

を結ぶベクトルをΔtで割って極限をとったものである。［竹之内脩］

3、曲線の長さ

2点A、Bを結ぶ曲線があるとき、この曲線上でA、Bの間に順に数多くの点

P₁, P₂,……, P_n-1 (A＝P₀, B＝P_n)

をとり、これらの点を次々と線分で結んで折れ線をつくる。

この折れ線の長さ（各線分の長さの和）が、

点のとり方をこの曲線上密になるようにしていったとき、

ある極限値に収束するならば、この曲線は長さがあるといい、この極限値を曲線の長さという。




　滑らかな曲線は長さを有し、その長さは次のようになる。


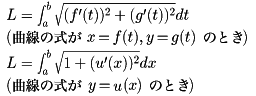
たとえば、円の場合は

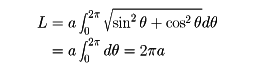
となり、周知の値を得る。

また、放物線y＝x²のx＝aからx＝b(a＜b)までの長さは、

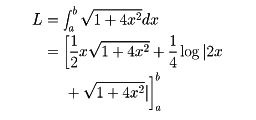
曲線の式がF(x, y)＝0の形で与えられているとき、

もしもある点で∂F/∂x＝0,∂F/∂y＝0が成り立っていると、

この点の近くでは一般にF(x, y)＝0をx＝f(t), y＝g(t)の形に表すことができない。

これを、この曲線の特異点という。



　曲線の式が与えられたとき、この曲線の概形を描くことを、曲線の追跡という。


このためには、曲線の存在する範囲や、特異点、漸近線などを調べるとよい。


　円のように両端がつながっている曲線を閉曲線という。

レムニスケートのように自分自身と交わりをもつ閉曲線もある。

レムニスケート

自分自身と交わりをもたない閉曲線を単純閉曲線、あるいはジョルダン閉曲線という。

ジョルダン閉曲線

ジョルダンは次のことを示した（1893）。


「平面内の単純閉曲線は、平面を内部と外部の二つの部分に分け、

内部の点と外部の点は、この曲線と交わることなしには結べない」。

これをジョルダンの曲線定理という。

内容は常識的であるが、

数学的に証明しようとするとむずかしい定理である。［竹之内脩］


『栗田稔著『いろいろな曲線』（1966・共立出版）』