1,積分法とは
図形の面積や曲線の長さを求める方法として発展し、これをさらに一般化し、
系統的に扱うようになったのが積分法である。
積分法は微分法の逆演算である。
すなわち、y=f(x)のグラフの下の面積S(x)を微分すればf(x)になる。
そこで、微分すればf(x)になるような関数を求め(これを不定積分という)、
それに両端の値を代入してその差を求める(これを定積分という)方法をとる。
このことによって図形の面積を求めたり、曲線の長さを求めたり、
微分方程式などの種々関連の問題を取り扱うことができるようになった。
しかし、積分の場合は、微分の場合と異なって、
不定積分が簡単に求まらないことが多い。
たとえば、
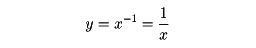
の下の面積、すなわち
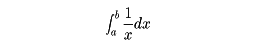
が対数の性質をもつことは微分積分法の発見以前から知られていた
(1647、サン・バンサンによる)。
このようにx n の形の不定積分が全然別種の関数を生み出す。
円弧の長さに関しては、
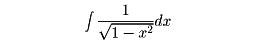
という積分が現れる。
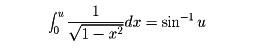
であることは現在では周知の事実だが、ニュートンは、
この被積分関数を二項級数に展開し、それを項別積分した級数をつくり、
それを反転して(すなわち逆関数の整級数をつくって)
sinθの級数展開を初めて得た(1665)。
ところでこれは、
sinθのような既知の関数になったために容易に結果がわかったが、
楕円の弧の長さを求めようとすると、
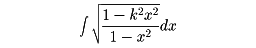
という積分が出てきて、
これがどんな関数になるかはわからなかった。
これは楕円積分と称されるものの一つである。
また、
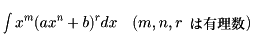
の形の積分も見かけは簡単であるが、m、n、rの間にぐあいよい関係がないと、
結果は初等関数(代数関数、指数関数、対数関数、三角関数、逆三角関数など、
微分積分学では基本的であると考えられる関数)では表せない。
そこで、このように、
「不定積分を求め、それの区間の両端における値の差が積分である」というように
積分を考えるのでなく、むしろ積分そのものを初めから定義して使おう、
という考えが19世紀になって生じた。
その始めはコーシーであるが(1820)、今日用いられているようなきちんとした形で
体系化したのはリーマンである(1854)。
しかし、当時すでに、フーリエ級数などと関連して、
この考えの枠に当てはまらない関数もいろいろあることがわかってきた。
またリーマン積分は極限演算に関して制約が多いことが難点であった。
19世紀後半には、いろいろな人が、このリーマンの与えた積分の定義を拡張しようと試みている
(ハルナック、シュトルツなど)。
そして20世紀初頭、ルベーグによる積分概念の発見により、
完全な形の積分法の体系ができあがったのである(1902)。
ルベーグ積分はリーマン積分を含み、極限演算などに関して好ましい性質を有している。
[竹之内脩]
関数f (x)が与えられたとき、F ′(x)=f (x)であるような関数F (x)を
f (x)の原始関数または不定積分(indefinite integral)という。
いま、F (x),G (x)がともにf x)の不定積分であるときは、
(F (x)-G (x))′=F ′(x)-G ′(x)=0となり、F (x)-G (x)は定数である。
そこで、f(x)の不定積分の一つをF(x)とするとき、
一般に不定積分を次のように表す。
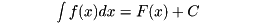
このC を積分定数という。
この式の意味は、C を一つ指定すれば、
それによって一つの不定積分が定まる、ということである。
ここで∫は、
ドイツの数学者・哲学者であるライプニッツの案出した記号で、
インテグラルと読む。
基本的な関数の不定積分と積分法の公式、それを用いた二、三の例を示す。
また、累乗の入った式の不定積分を順次簡単なものに変形していく式を漸化式という。
簡単な関数の不定積分であっても、その結果が初等関数を用いて表すことができない場合が多い。
楕円積分などがその例であるし、そのほか、次のような関数も、
簡単な関数だが、不定積分は初等関数にならない。
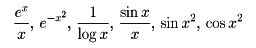
[竹之内脩]
関数f (x)は区間[a,b]で連続であるとする。
このとき、この区間上でf (x)を積分した値を、
f (x)のa からb までの定積分(definite integral)といって、
これを
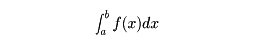
と表す。
a をこの定積分の下端、b を上端という。
また、xを積分変数というが、これは、他の任意の文字で置き換えてよい。
区間[a,b]で連続な関数f (x)は、そこで不定積分F (x)
すなわちF ′(x)=f (x)であるような関数F (x)をもつ。
そして、a からb までの定積分の値はF (b )-F (a )に等しい。
F (b )-F (a )のことを慣習的に[F(x)]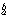 と表す。
と表す。
そうすれば、
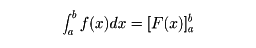 となる。
となる。
これを微分積分法の基本定理という。
このことの証明には、次のことが基礎となる。
すなわち、[a ,b ]で連続な関数f(x)に対して、
a ≦x≦b のとき、
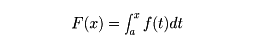
と置けば、F (x)は微分可能で、F ′(x)=f (x)である。
定積分の値を求めるには、
最後には、微分積分法の基本定理に持ち込まれるのが通常だが、
その前にいろいろな変形を施す。定積分の公式は、そのための公式である。
なお、定義からは、
a からb までの定積分の場合、a <b でなければならないが、
次のように定めておくと、区間についての加法性が成立して便利である。
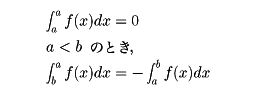
リーマン積分の意味から、次のことが知られる。
いま、区間[a ,b ]をn等分して、分点を順に
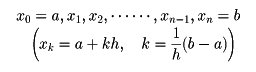
と置くとき、次の和
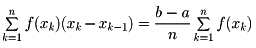
は、n→∞とするとき、
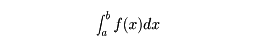
に収束する。
したがって、この和の値は定積分の近似値である。
これによって定積分の値の近似値を求め、
あるいは和の値の極限値を求める方法を区分求積法という。
定積分の近似値を求める方法としては、数値積分法がある。
[竹之内脩]
『吉田耕作著『私の微分積分法』(1981・講談社)
▽柴田敏男著『微積分に強くなる』(講談社・ブルーバックス)』
そして20世紀初頭、ルベーグによる積分概念の発見により、
完全な形の積分法の体系ができあがったのである(1902)。
ルベーグ積分はリーマン積分を含み、極限演算などに関して好ましい性質を有している。
[竹之内脩]
2,不定積分
f (x)の原始関数または不定積分(indefinite integral)という。
いま、F (x),G (x)がともにf x)の不定積分であるときは、
(F (x)-G (x))′=F ′(x)-G ′(x)=0となり、F (x)-G (x)は定数である。
そこで、f(x)の不定積分の一つをF(x)とするとき、
一般に不定積分を次のように表す。
このC を積分定数という。
この式の意味は、C を一つ指定すれば、
それによって一つの不定積分が定まる、ということである。
ここで∫は、
ドイツの数学者・哲学者であるライプニッツの案出した記号で、
インテグラルと読む。
基本的な関数の不定積分と積分法の公式、それを用いた二、三の例を示す。
また、累乗の入った式の不定積分を順次簡単なものに変形していく式を漸化式という。
簡単な関数の不定積分であっても、その結果が初等関数を用いて表すことができない場合が多い。
楕円積分などがその例であるし、そのほか、次のような関数も、
簡単な関数だが、不定積分は初等関数にならない。
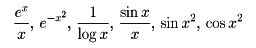
[竹之内脩]
3,定積分
このとき、この区間上でf (x)を積分した値を、
f (x)のa からb までの定積分(definite integral)といって、
これを
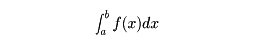
と表す。
a をこの定積分の下端、b を上端という。
また、xを積分変数というが、これは、他の任意の文字で置き換えてよい。
区間[a,b]で連続な関数f (x)は、そこで不定積分F (x)
すなわちF ′(x)=f (x)であるような関数F (x)をもつ。
そして、a からb までの定積分の値はF (b )-F (a )に等しい。
F (b )-F (a )のことを慣習的に[F(x)]
 と表す。
と表す。そうすれば、
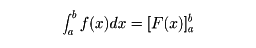 となる。
となる。これを微分積分法の基本定理という。
このことの証明には、次のことが基礎となる。
すなわち、[a ,b ]で連続な関数f(x)に対して、
a ≦x≦b のとき、
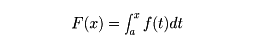
と置けば、F (x)は微分可能で、F ′(x)=f (x)である。
定積分の値を求めるには、
最後には、微分積分法の基本定理に持ち込まれるのが通常だが、
その前にいろいろな変形を施す。定積分の公式は、そのための公式である。
なお、定義からは、
a からb までの定積分の場合、a <b でなければならないが、
次のように定めておくと、区間についての加法性が成立して便利である。
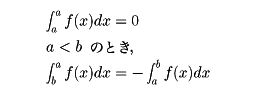
リーマン積分の意味から、次のことが知られる。
いま、区間[a ,b ]をn等分して、分点を順に
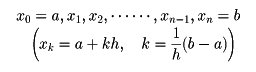
と置くとき、次の和
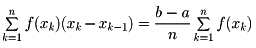
は、n→∞とするとき、
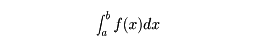
に収束する。
したがって、この和の値は定積分の近似値である。
これによって定積分の値の近似値を求め、
あるいは和の値の極限値を求める方法を区分求積法という。
定積分の近似値を求める方法としては、数値積分法がある。
[竹之内脩]
『吉田耕作著『私の微分積分法』(1981・講談社)
▽柴田敏男著『微積分に強くなる』(講談社・ブルーバックス)』

コメント
コメントを投稿