1、スピンとは
古典物理的な描像では粒子の自転による角運動量と考えられる。
運動する粒子の全角運動量は、軌道角運動量とこのスピン角運動量のベクトル和で表される。
原子スペクトルの多重項構造、
すなわち原子のエネルギー準位の微細構造の特徴を理解するために、
パウリは、原子の軌道を運動する電子に新しく二価性をもつ自由度を付加した。
クローニッヒRalph Kronig（1904―1995）、
ハウトスミット、ウーレンベックは、パウリの前記の考えを粒子の自転と解釈し、
自転に基づく角運動量の大きさが、
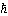（ディラック定数。プランク定数h を2πで割ったもので、エイチ・バーと読む）を単位にして1/2の値をとると考えた（第3軸成分は±1/2の値をとる）。
また電荷をもつものが回転していれば円電流が生じ、それに比例する磁気モーメントが予想できる。
この磁気モーメントの、ボーア磁子e
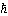/2mc（e は電子の電荷、m は同じく質量、c は光速度）を単位にして測った値をμとして、
このμと
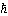を単位として測った角運動量との比をg因子とよぶ。このg因子を2とすると、トーマスの効果も考慮して、原子のエネルギー準位の微細構造、
さらにまたパウリの原理を加えることによって周期律を含めて、原子の諸特徴をみごとに説明できることがみいだされた。
［小川修三・植松恒夫］
2,スピン演算子
電子のスピンをどのように表すかという問題もパウリによって解決された。
まず電子の状態を記述する
シュレーディンガーの波動関数ψ(x )を2成分（2行1列の行列）
とすることによって、
この波動関数に演算する次のような演算子S （＝sx,sy,sz）、
を導入することができる。
この演算子は、電子が原子の周りを回転することによる
軌道角運動量L（＝Lx,Ly,Lz）と同じ代数的性質を備えており、角運動量としての資格をもっている。
しかし普通の軌道角運動量の値が
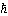を単位にして整数値であるのに対し、スピンは半整数の値をもつこと、
またg因子が軌道運動による部分については1であるのに対し、
スピンについては2であるなど、
単純な自転描像では、
かならずしも簡単に理解ができるとは限らない面がある。
これらの問題は、
ディラックの相対論的電子論の提唱をまって
解明されることになった。
一般にスピンの値が
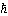を単位にして整数値をとる粒子をボソン、半整数値をとる粒子をフェルミオンという。
前者はボース‐アインシュタイン統計、後者はフェルミ‐ディラック統計に従う。
光子、グルーオン、ウィークボソンなどの力を媒介する
ゲージ粒子はスピンが1でボソン、物質を構成するクォークやレプトンは
スピンが1/2でフェルミオンである。
フェルミオンは同じ状態には1個の粒子しか存在できないというパウリの原理に従う。
力の統一にはフェルミオンとボソンの間を関連づける超対称性とよばれる対称性が重要な働きをすると考えられている。
［小川修三・植松恒夫］
3,核スピン
パウリの原理を満たす粒子（フェルミ‐ディラック粒子）であることが、
水素分子の比熱の問題の解明のなかで明らかになった。
もう一つの要素である中性子も、電荷が0という点を除いて陽子と同じ性質をもつ。
陽子・中性子を構成要素とする原子核は、
これら粒子のスピンや軌道運動の合成による核全体の角運動量をもつ。
これを核スピンというが、
同時に構成要素の磁気モーメントの和からなる核磁気モーメントができる。
この核磁気モーメントは、それと軌道電子の磁気モーメントとの相互作用により、
原子のエネルギー準位のずれ、すなわち準位の超微細構造を与える。
この構造から核のスピンを決定できる。
一方、核子は三つのクォークからなるが、
核子のスピンがその構成要素のクォークやグルーオンにいかに担われているかが、
偏極ビームおよび偏極ターゲットを用いた
核子の深非弾性散乱の実験で研究されている。
これまでのところ、素朴なクォーク模型の予想とは異なっており、
クォークやグルーオンの固有のスピン以外に
軌道角運動量からの寄与も含めて、核子スピンの起源の問題として追究されている。
［小川修三・植松恒夫］
『朝永振一郎著『スピンはめぐる』（1982・中央公論社） ▽亀淵迪・原康夫・小寺武康編、朝永振一郎著『角運動量とスピン』（1989・みすず書房） ▽久保謙一・鹿取謙二著『スピンと偏極』（1994・培風館） ▽宮下精二著『岩波講座 物理の世界 物質科学の展開7 量子スピン系――不確定性原理と秩序』（2006・岩波書店）』
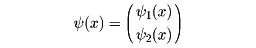
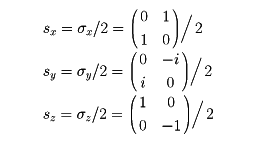
コメント
コメントを投稿