1,電車での出来事 電車の中では、 ふつうであれば夫婦や親子など 親密な関係にある人間しか 入ることを許されない密接距離や、 友人同士で用いられる個体距離のなかに 見知らぬ他人 が入りこんでくるということから、 別の規則が派生してくる。 私たちはたまたま電車で隣り合って座った人と 挨拶を交わたりしないし, ふつうは話しかけることもない。 私たちはあたかも 自分の 密接距離 や 個体距離 のなかに 人がいることに 気がつかないかのように、 それぞれ新聞や雑誌を読んだり、 ヘッドホンをつけ 音楽を聴いたり、携帯電話をチェックしたり、 ゲームをしたり,あるいは 目をつむって考えごとをしたりしている。 それはあたかも 物理的に失われた距離を心理的距離によって 埋め合わせているかのようである。 アメリカの社会学者 E. ゴフマン( 1922 ~ 82 )は, 公共空間のなかで人びとが示す このような態度を 儀礼的無関心 と呼んだ。 2、具体的に儀礼的無関心とは どのような状態で 行われるのか? 「そこで行なわれることは、 相手をちらっと見ることは見るが、 その時の表情は相手の存在を認識したことを 表わす程度にとどめるのが普通である。 そして、次の瞬間すぐに視線をそらし、 相手に対して特別の好奇心や 特別の意図がないことを示す。」 電車のなかで他の乗客にあからさまな 好奇心を向けることが 不適切とされるのはそのためである。 たとえば, 電車のなかで他の乗客をじろじろ眺めたり, 隣の人が読んでいる本を のぞきこんだりすることは不適切と感じられる。 例外は子どもである。 子どもは他の乗客を指差して 「あのおじさん変なマスクをしてる」 と言っても大目にみられるし, 逆に子どもに対してはじっと見つめることも, 話しかけることも許され
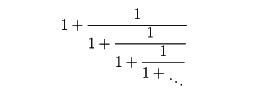
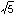 )/2 に収束する。
)/2 に収束する。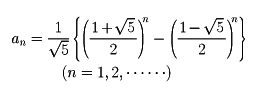

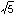 )/2 に収束する。
)/2 に収束する。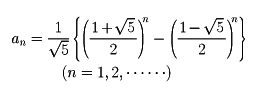
コメント
コメントを投稿