ポテンシャルエネルギー

1、ポテンシャルエネルギーとは

力の場の各点に位置のエネルギーが定まる場合に、

それをポテンシャルまたはポテンシャル・エネルギーとよぶ。

「ポテンシャル」は潜在的の意。

運動の勢いとして顕在する運動エネルギーに対していう。

両者の和が一定で、エネルギーは顕在したり潜在したり

互いに移り変わることができるのは、投げたボールやジェット・コースターなどの例にみられるとおりである。

力学的エネルギー=運動エネルギー+ポテンシャルエネルギー

［江沢　洋］

2,力の場とポテンシャル

質点の受ける力が空間の場所により定まっているとき、その空間を力の場という

（たとえば、太陽の周りの重力の場、ただし、太陽は空間に静止しているものとする）。



力の場に基準点Aをとり、そこに静止している質量m の質点を静かに

（速度、加速度がゼロ、したがって無限の時間をかけて）

別の点Pまで運ぶ仕事量W (A-Γ-P)が途中の道筋によらず、Pの位置P(x,y,z)のみで定まる場合に限り

　　W(A-Γ-P)＝W(P)＝W(x,y,z)

なる関数をこの力の場における質点mのポテンシャルとよび、この種の場を保存力の場という。

Pまで運ぶ仕事が途中の道筋によって違うということがおこるのは、

たとえば力の場が渦を巻いている場合である（下図）。

［江沢　洋］

3,ポテンシャルの場

保存力の場における質点m のポテンシャルは

空間の各点で値（スカラー）が定まっているので、これも場である。

座標の原点Oに固定された点電荷Qがあり、質点mも電荷qをもっているとし、

二つの電荷は同符号とすれば、質点mにはOを中心とし逆二乗の法則に従う斥力が働く。

この力は保存力であって、ポテンシャルの場W (x,y,z)をもつことが証明される。

質点mに働く力は斥力で、点Oに近づくほど強くなるから、

mをOの近くまで運ぼうとすれば、それだけ大きな仕事をしなければならない。

それゆえz＝0の面上に限定してW(x,y,0)の値をグラフにすると

上の図の左のような山の形（ポテンシャルの山）ができる。

これがポテンシャルの場の一つの表し方である。

この山はまた、等高線（等ポテンシャル線とよぶ）をxy面に描くことにしても表現できる

（z＝0に限定しなければ等ポテンシャル「面」で表現することになる）。

ポテンシャルの山は、もとの力の場も表現している。



実際、質点mを等ポテンシャル線に沿って運ぶのに仕事は不要だから、

上の図の右の点Pで質点mに働く力は等ポテンシャル線に沿う成分をもたないことが、まずわかる。


力は等ポテンシャル線に垂直な成分をもつのみだから、その成分をf(P)と書いてみる。

質点mを静かに山の上方の点P'まで引き上げるには、

質点に－f (P)の力を加えるので、－f (P)・PP'だけの仕事をすることになる。

これがポテンシャルの増加

　　W (P')－W (P)

になるわけだから、



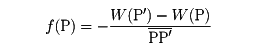
が導かれる（正確にはP'→Pの極限をとる）。

つまり力は、ポテンシャルの山からその勾配(こうばい)として求められる。

このことは、いま考えた電荷の間の力に限らず一般にいえる。

［江沢　洋］


『戸田盛和著『物理入門コース1　力学』（1982・岩波書店）　

▽原島鮮著『質点の力学』改訂版（1984・裳華房）　

▽S・ガシオロウィッツ著、林武美・北門新作訳『量子力学1』（1998・丸善）　

▽江沢洋著『量子力学1、2』（2002・裳華房）　

▽江沢洋著『力学――高校生・大学生のために』（2005・日本評論社）』