ドップラー効果

1,ドップラー効果とは

警笛を鳴らしながら列車が線路のわきに立つ観測者の前を走り過ぎると、

そのとたんに警笛の音が低くなったように聞こえる。

振動数ν₀の音波を放つ音源と、この音を聴く観測者の、

一方または両方が運動しているときには、

観測者の聴く音の振動数νは、一般には音源の振動数ν₀と同じ値をもたない。
これを（音波の）ドップラー効果という。



音源から観測者に向かう方向をn 方向とする。

観測者の速度u のn 方向成分をu_n、音源の速度v のn 方向成分をv_nとし、

静止座標系における音波の速度をc とする。


二つの振動数の比は

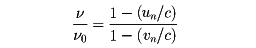
である。


とくに、初めに記した例で、列車が近づいてくるときには

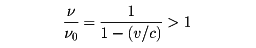
遠ざかるときには

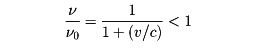
となる。




　音源や観測者が運動しているときには、

時間間隔（周期）T₀ごとに音源から放たれた音波が

観測者に届くまでに通過する距離が各周期ごとに

一定量ずつ減るか増えるかするために、

観測者の聴く音波の周期T はT₀と同じではない。


したがって、

周期の逆数である振動数νとν₀も異なる値をもつことになる。

また、音源とともに運動する座標系、

観測者とともに運動する座標系、

および静止座標系で測った位置座標の間の関係は、

ガリレイ変換によって与えられる。


音源から放たれてn 方向に伝わる音波の位相の式を

三つの座標系について書くと、振動数の比ν/ν₀の式が得られる。




　まっすぐな道路を速度vで進む車から時間間隔T₀を置いて次々に伝書鳩を放ち、

この道路を速度u で先行する車を追わせる。

伝書鳩の速度をcとする。

先行する車には、時間間隔Tごとに伝書鳩が着く。

T とT₀の間には

　　vT₀＝c (T₀－T )＋uT

の関係がある。



T₀、T の逆数をν₀、νと書くと

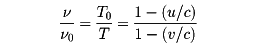
となる。

前出の式はこれと同じ式である。


［飼沼芳郎］

2,光波のドップラー効果とは

特殊相対性理論の、ローレンツ変換を用いて論じられる。

音波の場合との相違点は、どの座標系（慣性系）についても

真空中の光速度c₀が同一の値をもつことである。


光源の座標系が、観測者の座標系に対して速度Vで

並進運動をする場合には、光源の放つ振動数ν₀の光波が

n 方向に進み、振動数νの光波として観測者に観測される。

二つの振動数の比は

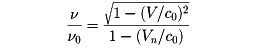
ここに、V_nは速度Vのn方向成分である。


とくに、V がn に平行の場合には

Vがn に反平行の場合には

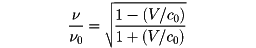
である。


これらの比は、(V /c₀)²が1に比して無視できる場合には、

音波のドップラー効果の式と同じ形の式となる。

これを縦のドップラー効果という。



　Vがn に垂直のときには

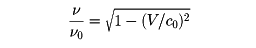
となる。この振動数の比は、V が大きく、

(V /c₀)²が1に比して無視できぬ場合にだけ1と異なる値をもつ。

これは光波にだけみられる効果で、横のドップラー効果とよばれる。


この効果は、「走っている時計は遅れる」という

特殊相対性理論でよく知られた現象の一例である。



［飼沼芳郎］

3,応用

オーストリアのJ・C・ドップラーが1842年にドップラー効果の着想を得たのち、

音波や光波の分野でこの効果について数多くの研究が行われ、

この効果はさまざまの方面に応用されてきた。


気体の原子は走りながら光を放つ。

気体原子の速度はマクスウェル分布に従って

いろいろの値をとるので、ドップラー効果により、


原子スペクトルの振動数は気体の温度に比例する幅にわたって分布する。

これをスペクトル線のドップラー幅という。

銀河系外の星雲の放つ光の連続スペクトルには

数本の暗線（吸収線）が観察される。

この暗線の振動数は、

実験室内で観察される原子スペクトルの対応する

線の振動数に比べると赤のほうに偏移している。



ハッブルはこの赤方偏移がドップラー効果によって生ずると考えて、

銀河系外の星雲は、

遠方の星雲ほど大きな速度で遠ざかっているとし、

宇宙は膨張しているという解釈に到達した。


メスバウアー効果の実験では、無反跳γ(ガンマ)線の線源を

一定速度で動かしたときにおこるγ線のドップラー効果が用いられる。


路上を走行する自動車の速度の計測には、ドップラーレーダーが用いられ、

センチメートル波の電波が車で反射したときの

ドップラー効果が利用されている。



［飼沼芳郎］