1,微分方程式とは
変数x と、その関数y との関係を、x 、y や
その導関数を含む方程式の形で表したものを微分方程式という。
微分方程式は、独立変数が一つの常微分方程式と、
独立変数が2個以上で偏導関数を含む
偏微分方程式とに分けられる。
ここでは、微分方程式の理論の歴史的形成について述べる。
ガリレオが落体の運動を研究していて、
時間tの間に落下する距離をx (t )とすると、
加速度
x ″(t )=g (一定)
であることを発見し、
その解
を得たのが、微分方程式が解かれた最初であるといわれている。
これはニュートンやライプニッツの微分積分の始まる50年も前(1680ころ)である。
微分方程式が本格的に研究されるのはニュートン以後で、
まず18世紀前半は、特殊な方程式をそれ特有の方法で解いていた(求積法)が、
後半には級数による解法が用いられるようになる。
1820年ごろコーシーが、微分方程式の解の存在を調べる必要があることを強調して、
理論的な研究が始まり、
さらに、ポアンカレの漸近級数による解法などから、
常微分方程式の解の定性的な研究が始まった。
偏微分方程式は18世紀の中ごろまでは現れない。
ダランベールが、x 軸上の区間[0,1]に張られた弦の振動の方程式は、
時間t、場所xにおける変位をu (t ,x )とすると、
で表されることを示し、その解は
u (t ,x ) =f (x -ct )+g (x +ct )
(f ,g は任意の関数)
となることを示している。
さらに、ベルヌーイなどにより、ポテンシャルの方程式や
熱伝導の方程式などが導入され、
フーリエになって、フーリエ級数による解法が応用上成功し、フーリエ級数論の発端となった。
[洲之内治男]
2,物理現象と微分方程式
これを微分方程式の形に表現することができる。
たとえば、運動の法則は、質点の座標の時間に関する二階微分方程式として表され、
電磁場に関する法則は、電場と磁場の時間と空間に関する
一階の連立偏微分方程式、すなわちマクスウェル方程式の形をとっている。
これらの法則に基づいて物理現象を量的に理解するためには、
法則を数学的に表現した微分方程式を解かなければならない。
微分方程式の一般解は任意定数または任意関数を含んでいる。
これらの任意定数または任意関数を決定するには、対象とする物理現象の物理的条件を用いればよい。
ニュートンの運動の法則は、
力の作用のもとで速度がどのように変化するかを与えているにすぎないため
運動法則に対応する微分方程式の解には、速度の変化が同じであっても位置や
速度のさまざまな運動に対応するものが含まれている。
この解の多様性が一般解の2個の積分定数である。
したがって微分方程式の解は、任意の時刻の質点の位置や速度を物理条件として与えることによって初めて一義的に定まる。
偏微分方程式の一般解に含まれている任意関数は、ある特定の領域における
解の値を与えることによって定まる場合が多い。
このような条件を与えられて解かれる微分方程式を境界値問題という。
この場合、物理的条件は特定領域の関数値すなわち境界値によって与えられる。
[田中 一]
リンク
リンク

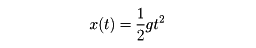
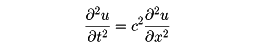
コメント
コメントを投稿